转载：向量数据库 – 编程续想

也许你最近可能听过这样的新闻，某向量数据库的初创公司刚写好 PPT，就获得了几千万的投资，某公司的开源的向量数据库因其代码的简陋而登上了 Hackernews 等等。在过去几个月时间中， AI 应用的发展如火如荼，带动了 AI 应用技术栈上下游的火爆，而向量数据库就是其中最热门的之一。

笔者最近因为开发 ChatFiles 和 VectorHub 两款开源项目的需要从而对向量数据库（Vector Database）进行了学习，在对主流的向量数据库和搜索算法有了大概的了解后，笔者决定将这些知识整理成一篇文章，希望能够帮助到大家。

GPT 的缺陷

过去几个月的时间，我们正处于人工智能的革命中，其中最耀眼的莫过于 GPT-3.5/4 的横空出世，而 GPT-3.5/4 带给我们无限震撼的同时，其天然的缺陷和诸多的限制也让开发者头痛不已，例如其输入端上下文（tokens）大小的限制困扰着很多的开发者和消费者，像 gpt-3.5-turbo 模型它的限制是 4K tokens(～3000字)，这意味着使用者最多只能输入 3000 字给 GPT 来理解和推理答案。

有人可能会疑惑，我使用的 ChatGPT 是有对话记忆功能的，既然它可以做到聊天记忆，那么它的输入端 token 有限制也没什么关系，只要我将给 ChatGPT 的文字内容拆分成多次输入，它自然就可以记住我之前的对话，从而做到解除 token 限制。

这个想法是不太正确的，GPT 作为 LLM 模型是没有记忆功能的，所谓的记忆功能只是开发者将对话记录存储在内存或者数据库中，当你发送消息给 gpt 模型时，程序会自动将最近的几次对话记录（基于对话的字数限制在 4096 tokens 内）通过 prompt 组合成最终的问题，并发送给 ChatGPT。简而言之，如果你的对话记忆超过了 4096 tokens，那么它就会忘记之前的对话，这就是目前 GPT 在需求比较复杂的任务中无法克服的缺陷。

目前，不同模型对于 token 的限制也不同，gpt-4 是 32K tokens 的限制，而目前最大的 token 限制是 Claude 模型的 100K，这意味可以输入大约 75000 字的上下文给 GPT，这也意味着 GPT 直接理解一部《哈利波特》的所有内容并回答相关问题。

但这样就能解决我们所有的问题了吗？答案是否定的，首先 Claude 给出的例子是 GPT 处理 72K tokens 上下文的响应速度是 22 秒。如果我们拥有 GB 级别或更大的文档需要进行 GPT 理解和问答，目前的算力很难带来良好体验，更关键的是目前 GPT API 的价格是按照 tokens 来收费的，所以输入的上下文越多，其价格越按昂贵。

这种情况有点类似于早期开发者面对内存只有几 MB 甚至几 KB 时期开发应用的窘境，一是‘内存’昂贵，二是‘内存’太小，所以在 GPT 模型在性能、成本、注意力机制等方面有重大革命性进展前，开发者不得不面对的绕过 GPT tokens 限制的难题。

向量数据库的崛起

在 GPT 模型的限制下，开发者们不得不寻找其他的解决方案，而向量数据库就是其中之一。向量数据库的核心思想是将文本转换成向量，然后将向量存储在数据库中，当用户输入问题时，将问题转换成向量，然后在数据库中搜索最相似的向量和上下文，最后将文本返回给用户。

当我们有一份文档需要 GPT 处理时，例如这份文档是客服培训资料或者操作手册，我们可以先将这份文档的所有内容转化成向量（这个过程称之为 Vector Embedding），然后当用户提出相关问题时，我们将用户的搜索内容转换成向量，然后在数据库中搜索最相似的向量，匹配最相似的几个上下文，最后将上下文返回给 GPT。这样不仅可以大大减少 GPT 的计算量，从而提高响应速度，更重要的是降低成本，并绕过 GPT 的 tokens 限制。

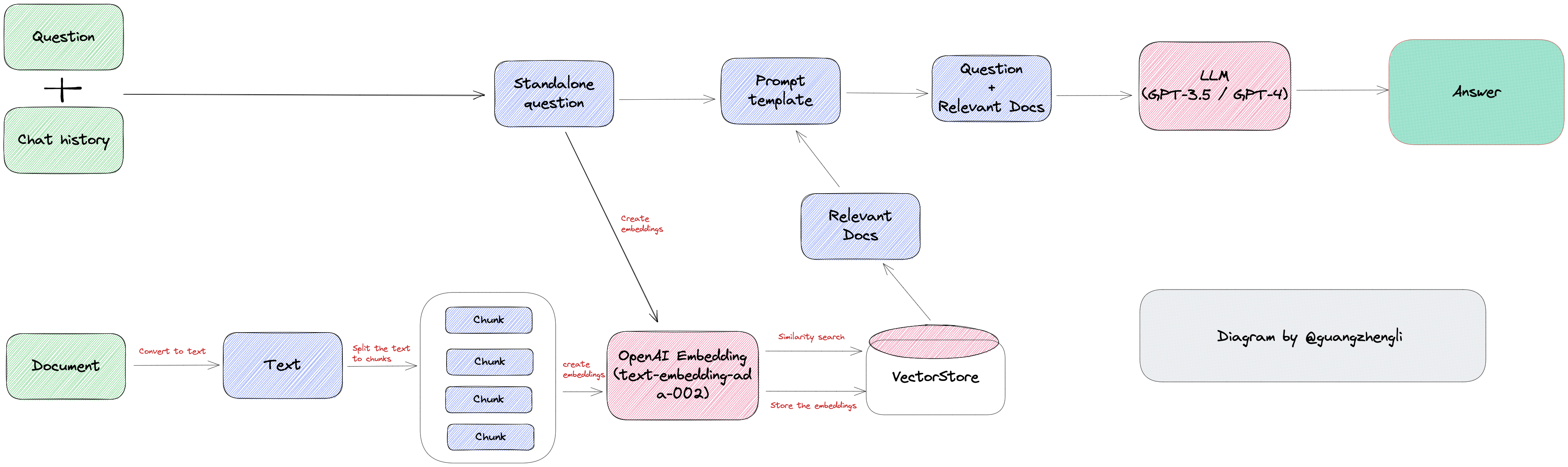
再比如我们和 ChatGPT 之间有一份很长的对话，我们可以将所有对话以向量的方式保存起来，当我们提问给 ChatGPT 时，我们可以将问题转化为向量对过去所有的聊天记录进行语义搜索，找到与当前问题最相关的‘记忆’，一起发送给 ChatGPT，极大的提高 GPT 的输出质量。

向量数据库的作用当然不止步于文字语义搜索，在传统的 AI 和机器学习场景中，还包含人脸识别、图像搜索、语音识别等功能，但不可否认的是，这一轮向量数据库的火爆，正是因为它对于 AI 获得理解和维护长期记忆以执行复杂任务时有非常大的帮助。例如你可以试试 LangChainJs 的文档搜索/Q&A 功能感受它的魅力，或者可以试试笔者的开源项目 VectorHub 和 ChatFiles，可以上传一份文档或者基于一份网页文档，然后询问文档相关问题。这些功能都是基于 Vector Embedding 和向量数据库的产品。

Vector Embeddings

对于传统数据库，搜索功能都是基于不同的索引方式（B Tree、倒排索引等）加上精确匹配和排序算法（BM25、TF-IDF）等实现的。本质还是基于文本的精确匹配，这种索引和搜索算法对于关键字的搜索功能非常合适，但对于语义搜索功能就非常弱。

例如，如果你搜索“小狗”，那么你只能得到带有“小狗”关键字相关的结果，而无法得到“柯基”、“金毛”等结果，因为“小狗”和“金毛”是不同的词，传统数据库无法识别它们的语义关系，所以传统的应用需要人为的将“小狗”和“金毛”等词之间打上特征标签进行关联，这样才能实现语义搜索。而如何将生成和挑选特征这个过程，也被称为 Feature Engineering (特征工程)，它是将原始数据转化成更好的表达问题本质的特征的过程。

但是如果你需要处理非结构化的数据，就会发现非结构化数据的特征数量会开始快速膨胀，例如我们处理的是图像、音频、视频等数据，这个过程就变得非常困难。例如，对于图像，可以标注颜色、形状、纹理、边缘、对象、场景等特征，但是这些特征太多了，而且很难人为的进行标注，所以我们需要一种自动化的方式来提取这些特征，而这可以通过 Vector Embedding 实现。

Vector Embedding 是由 AI 模型（例如大型语言模型 LLM）生成的，它会根据不同的算法生成高维度的向量数据，代表着数据的不同特征，这些特征代表了数据的不同维度。例如，对于文本，这些特征可能包括词汇、语法、语义、情感、情绪、主题、上下文等。对于音频，这些特征可能包括音调、节奏、音高、音色、音量、语音、音乐等。

例如对于目前来说，文本向量可以通过 OpenAI 的 text-embedding-ada-002 模型生成，图像向量可以通过 clip-vit-base-patch32 模型生成，而音频向量可以通过 wav2vec2-base-960h 模型生成。这些向量都是通过 AI 模型生成的，所以它们都是具有语义信息的。

例如我们将这句话 “Your text string goes here” 用 text-embedding-ada-002 模型进行文本 Embedding，它会生成一个 1536 维的向量，得到的结果是这样：“-0.006929283495992422, -0.005336422007530928, ... -4547132266452536e-05,-0.024047505110502243”，它是一个长度为 1536 的数组。这个向量就包含了这句话的所有特征，这些特征包括词汇、语法，我们可以将它存入向量数据库中，以便我们后续进行语义搜索。

特征和向量

虽然向量数据库的核心在于相似性搜索(Similarity Search)，但在深入了解相似性搜索前，我们需要先详细了解一下特征和向量的概念和原理。

我们先思考一个问题？为什么我们在生活中区分不同的物品和事物？

如果从理论角度出发，这是因为我们会通过识别不同事物之间不同的特征来识别种类，例如分别不同种类的小狗，就可以通过体型大小、毛发长度、鼻子长短等特征来区分。如下面这张照片按照体型排序，可以看到体型越大的狗越靠近坐标轴右边，这样就能得到一个体型特征的一维坐标和对应的数值，从 0 到 1 的数字中得到每只狗在坐标系中的位置。

然而单靠一个体型大小的特征并不够，像照片中哈士奇、金毛和拉布拉多的体型就非常接近，我们无法区分。所以我们会继续观察其它的特征，例如毛发的长短。

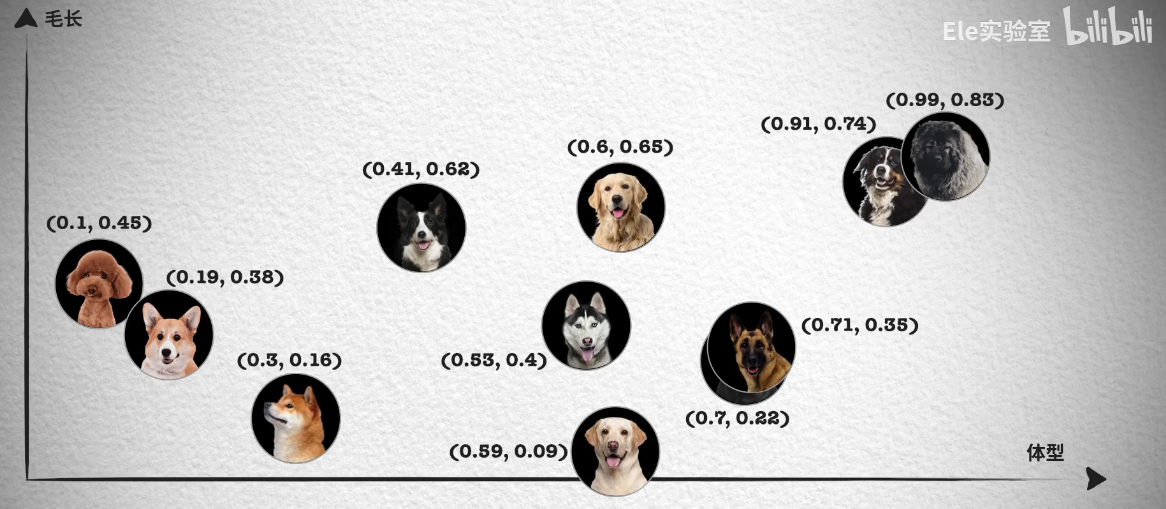
这样每只狗对应一个二维坐标点，我们就能轻易的将哈士奇、金毛和拉布拉多区分开来，如果这时仍然无法很好的区分德牧和罗威纳犬。我们就可以继续再从其它的特征区分，比如鼻子的长短，这样就能得到一个三维的坐标系和每只狗在三维坐标系中的位置。

在这种情况下，只要特征足够多，就能够将所有的狗区分开来，最后就能得到一个高维的坐标系，虽然我们想象不出高维坐标系长什么样，但是在数组中，我们只需要一直向数组中追加数字就可以了。

实际上，只要维度够多，我们就能够将所有的事物区分开来，世间万物都可以用一个多维坐标系来表示，它们都在一个高维的特征空间中对应着一个坐标点。

那这和相似性搜索 (Similarity Search) 有什么关系呢？你会发现在上面的二维坐标中，德牧和罗威纳犬的坐标就非常接近，这就意味着它们的特征也非常接近。我们都知道向量是具有大小和方向的数学结构，所以可以将这些特征用向量来表示，这样就能够通过计算向量之间的距离来判断它们的相似度，这就是相似性搜索。

上面这几张图片和详细解释来源于这个视频，这个视频系列也包含了部分下方介绍的相似性搜索算法。如果你对这个向量数据库感兴趣，非常推荐看看这个视频。

相似性搜索 (Similarity Search)

既然我们知道了可以通过比较向量之间的距离来判断它们的相似度，那么如何将它应用到真实的场景中呢？如果想要在一个海量的数据中找到和某个向量最相似的向量，我们需要对数据库中的每个向量进行一次比较计算，但这样的计算量是非常巨大的，所以我们需要一种高效的算法来解决这个问题。

高效的搜索算法有很多，其主要思想是通过两种方式提高搜索效率：

减少向量大小——通过降维或减少表示向量值的长度。
缩小搜索范围——可以通过聚类或将向量组织成基于树形、图形结构来实现，并限制搜索范围仅在最接近的簇中进行，或者通过最相似的分支进行过滤。

我们首先来介绍一下大部分算法共有的核心概念，也就是聚类。

K-Means 和 Faiss

我们可以在保存向量数据后，先对向量数据先进行聚类。例如下图在二维坐标系中，划定了 4 个聚类中心，然后将每个向量分配到最近的聚类中心，经过聚类算法不断调整聚类中心位置，这样就可以将向量数据分成 4 个簇。每次搜索时，只需要先判断搜索向量属于哪个簇，然后再在这一个簇中进行搜索，这样就从 4 个簇的搜索范围减少到了 1 个簇，大大减少了搜索的范围。

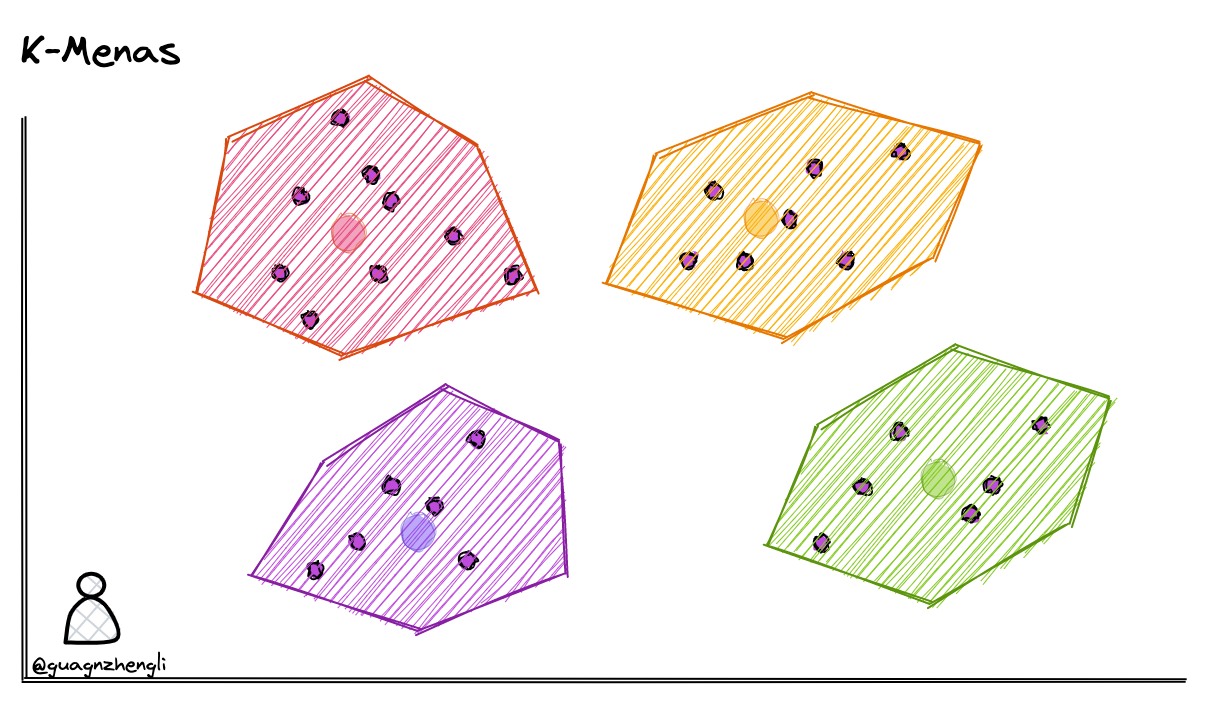
常见的聚类算法有 K-Means，它可以将数据分成 k 个类别，其中 k 是预先指定的。以下是 k-means 算法的基本步骤：

选择 k 个初始聚类中心。
将每个数据点分配到最近的聚类中心。
计算每个聚类的新中心。
重复步骤 2 和 3，直到聚类中心不再改变或达到最大迭代次数。

但是这种搜索方式也有一些缺点，例如在搜索的时候，如果搜索的内容正好处于两个分类区域的中间，就很有可能遗漏掉最相似的向量。

现实情况中，向量的分布也不会像图中一样区分的那么明显，往往区域的边界是相邻的，就像下图 Faiss 算法一样。

我们可以将向量想象为包含在 Voronoi 单元格中 – 当引入一个新的查询向量时，首先测量其与质心 (centroids) 之间的距离，然后将搜索范围限制在该质心所在的单元格内。

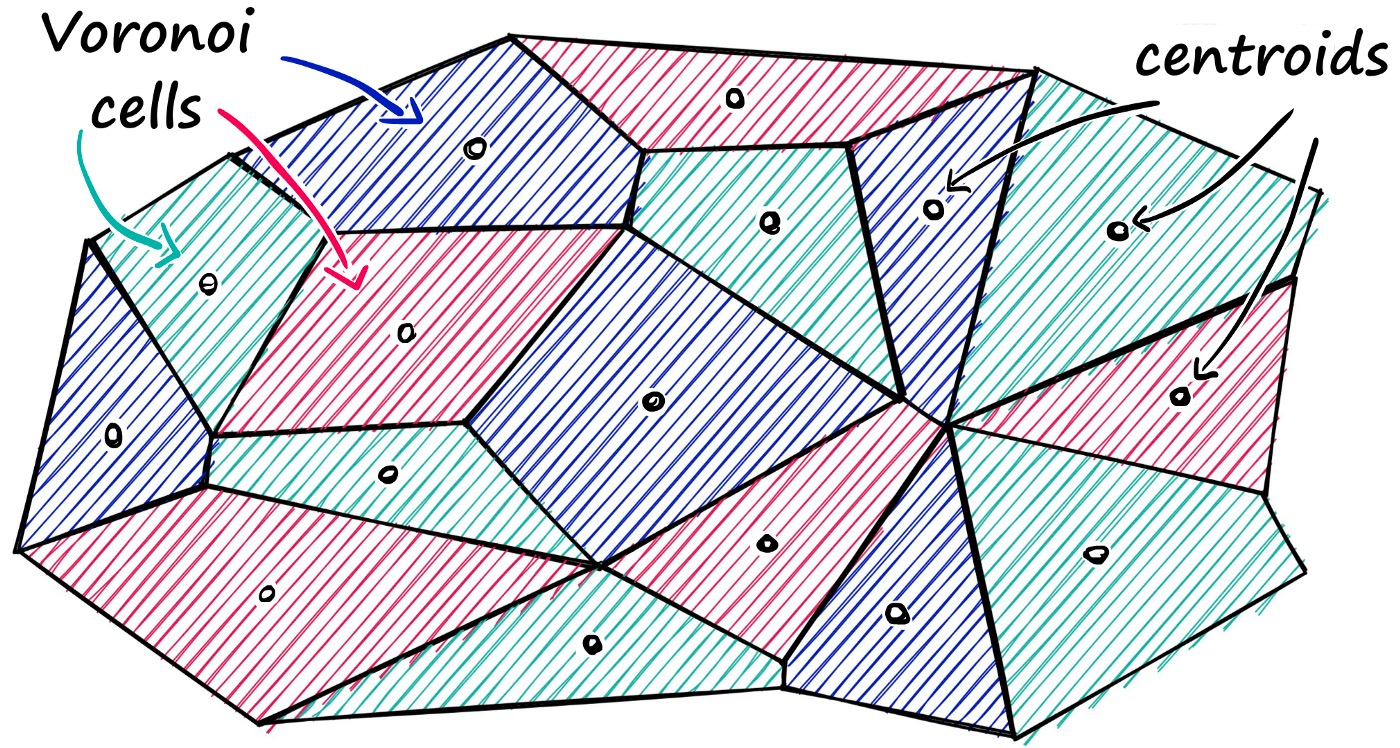
那么为了解决搜索时可能存在的遗漏问题，可以将搜索范围动态调整，例如当 nprobe = 1 时，只搜索最近的一个聚类中心，当 nprobe = 2 时，搜索最近的两个聚类中心，根据实际业务的需求调整 nprobe 的值。

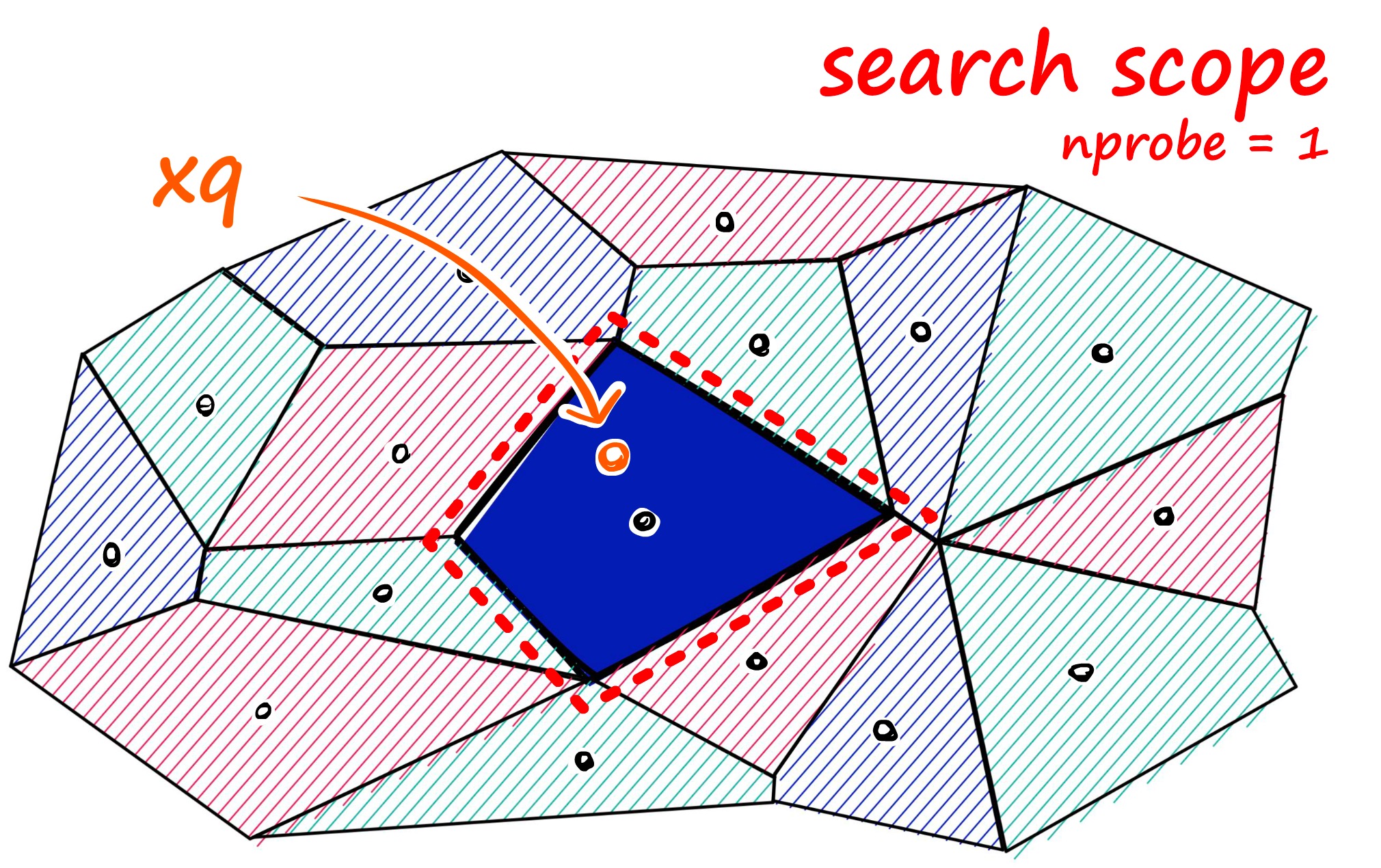
实际上，除了暴力搜索能完美的搜索出最相邻，所有的搜索算法只能在速度和质量还有内存上做一个权衡，这些算法也被称为近似最相邻（Approximate Nearest Neighbor）。

Product Quantization (PQ)

在大规模数据集中，聚类算法最大的问题在于内存占用太大。这主要体现在两个方面，首先因为需要保存每个向量的坐标，而每个坐标都是一个浮点数，占用的内存就已经非常大了。除此之外，还需要维护聚类中心和每个向量的聚类中心索引，这也会占用大量的内存。

对于第一个问题，可以通过量化 (Quantization) 的方式解决，也就是常见的有损压缩。例如在内存中可以将聚类中心里面每一个向量都用聚类中心的向量来表示，并维护一个所有向量到聚类中心的码本，这样就能大大减少内存的占用。

但这仍然不能解决所有问题，在前面一个例子中，在二维坐标系中划分了聚类中心，同理，在高维坐标系中，也可以划定多个聚类中心点，不断调整和迭代，直到找到多个稳定和收敛的中心点。

但是在高维坐标系中，还会遇到维度灾难问题，具体来说，随着维度的增加，数据点之间的距离会呈指数级增长，这也就意味着，在高维坐标系中，需要更多的聚类中心点将数据点分成更小的簇，才能提高分类的质量。否者，向量和自己的聚类中心距离很远，会极大的降低搜索的速度和质量。

但如果想要维持分类和搜索质量，就需要维护数量庞大的聚类中心。随之而来会带来另一个问题，那就是聚类中心点的数量会随着维度的增加而指数级增长，这样会导致我们存储码本的数量极速增加，从而极大的增加了内存的消耗。例如一个 128 维的向量，需要维护 2^64 个聚类中心才能维持不错的量化结果，但这样的码本存储大小已经超过维护原始向量的内存大小了。

解决这个问题的方法是将向量分解为多个子向量，然后对每个子向量独立进行量化，比如将 128 维的向量分为 8 个 16 维的向量，然后在 8 个 16 维的子向量上分别进行聚类，因为 16 维的子向量大概只需要 256 个聚类中心就能得到还不错的量化结果，所以就可以将码本的大小从 2^64 降低到 8 * 256 = 2048 个聚类中心，从而降低内存开销。

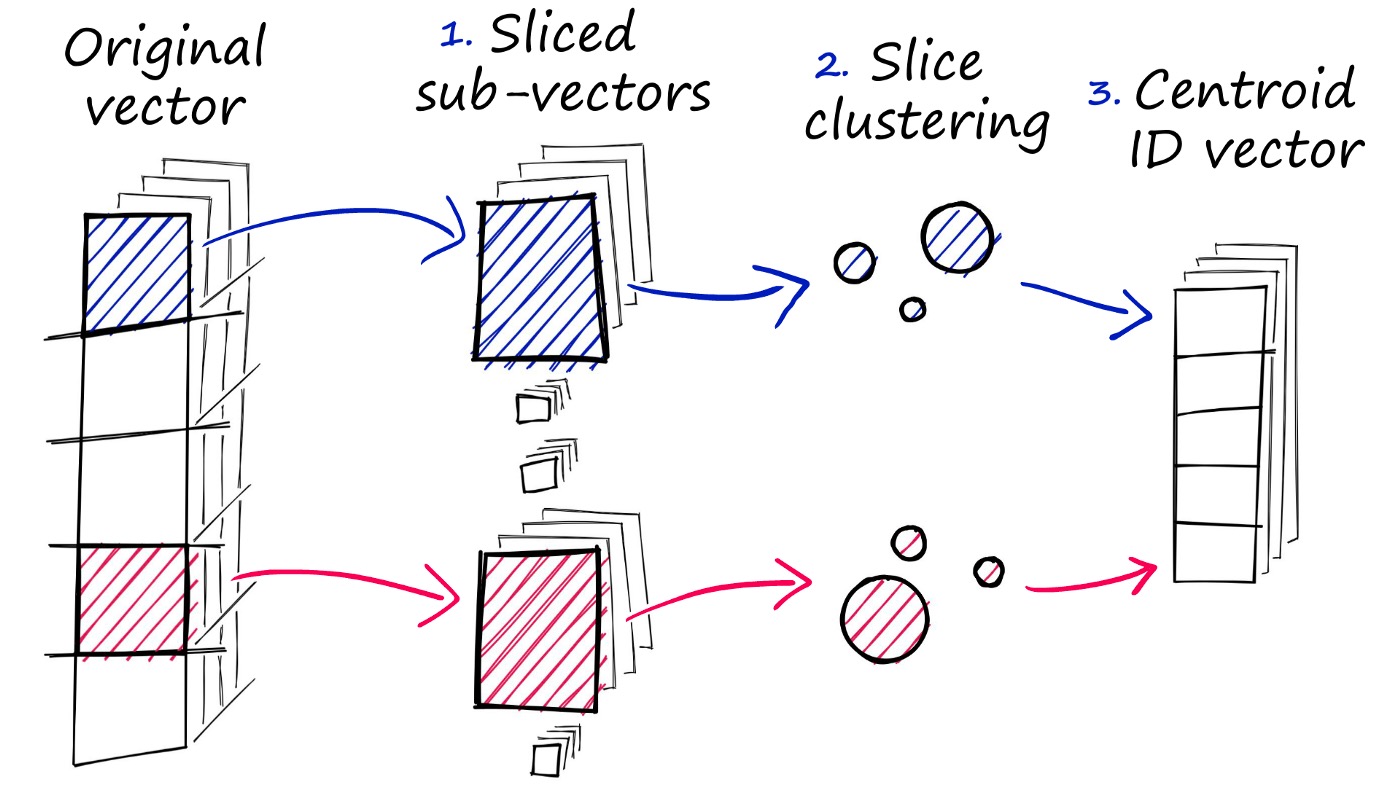
而将向量进行编码后，也将得到 8 个编码值，将它们拼起来就是该向量的最终编码值。等到使用的时候，只需要将这 8 个编码值，然后分别在 8 个子码本中搜索出对应的 16 维的向量，就能将它们使用笛卡尔积的方式组合成一个 128 维的向量，从而得到最终的搜索结果。这也就是乘积量化（Product Quantization）的原理。

使用 PQ 算法，可以显著的减少内存的开销，同时加快搜索的速度，它唯一的问题是搜索的质量会有所下降，但就像我们刚才所讲，所有算法都是在内存、速度和质量上做一个权衡。

Hierarchical Navigable Small Worlds (HNSW)

除了聚类以外，也可以通过构建树或者构建图的方式来实现近似最近邻搜索。这种方法的基本思想是每次将向量加到数据库中的时候，就先找到与它最相邻的向量，然后将它们连接起来，这样就构成了一个图。当需要搜索的时候，就可以从图中的某个节点开始，不断的进行最相邻搜索和最短路径计算，直到找到最相似的向量。

这种算法能保证搜索的质量，但是如果图中所以的节点都以最短的路径相连，如图中最下面的一层，那么在搜索的时候，就同样需要遍历所有的节点。

解决这个问题的思路与常见的跳表算法相似，如下图要搜索跳表，从最高层开始，沿着具有最长“跳过”的边向右移动。如果发现当前节点的值大于要搜索的值-我们知道已经超过了目标，因此我们会在下一级中向前一个节点。

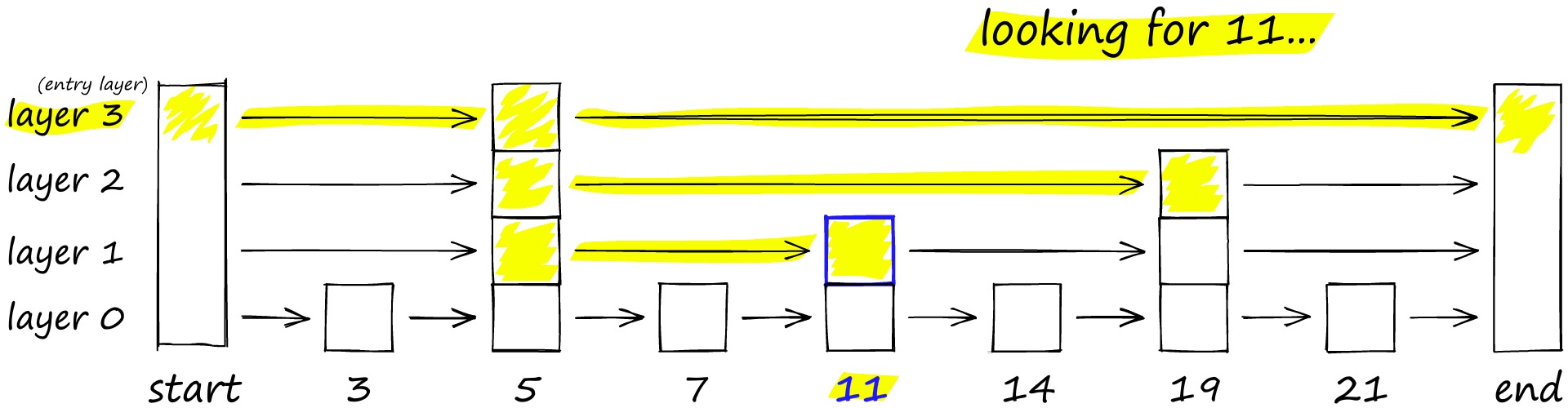
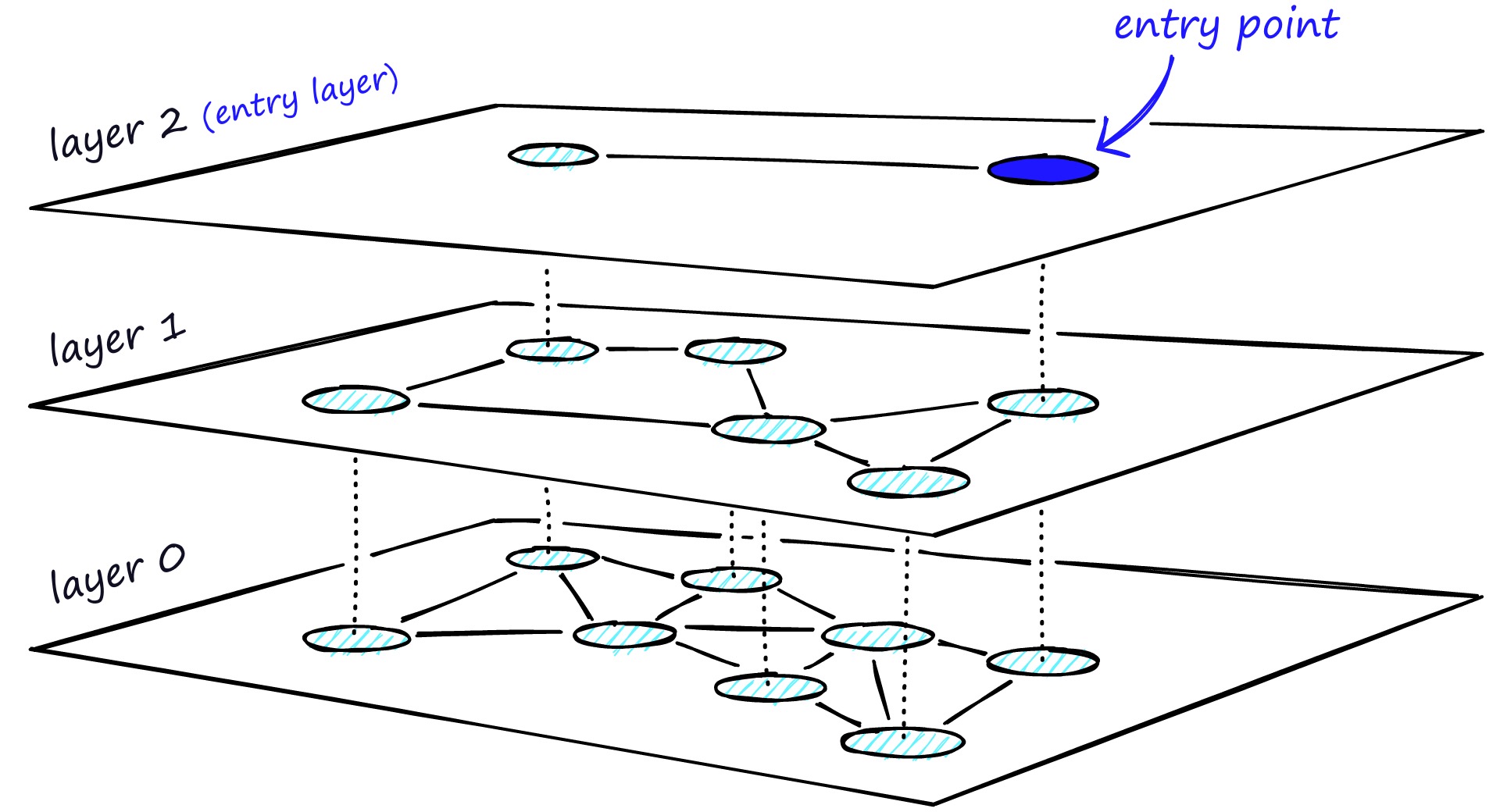
HNSW 继承了相同的分层格式，最高层具有更长的边缘（用于快速搜索），而较低层具有较短的边缘（用于准确搜索）。

具体来说，可以将图分为多层，每一层都是一个小世界，图中的节点都是相互连接的。而且每一层的节点都会连接到上一层的节点，当需要搜索的时候，就可以从第一层开始，因为第一层的节点之间距离很长，可以减少搜索的时间，然后再逐层向下搜索，又因为最下层相似节点之间相互关联，所以可以保证搜索的质量，能够找到最相似的向量。

如果你对跳表和 HNSW 感兴趣，可以看看这个视频。

HNSW 算法是一种经典的空间换时间的算法，它的搜索质量和搜索速度都比较高，但是它的内存开销也比较大，因为不仅需要将所有的向量都存储在内存中。还需要维护一个图的结构，也同样需要存储。所以这类算法需要根据实际的场景来选择。

Locality Sensitive Hashing (LSH)

局部敏感哈希（Locality Sensitive Hashing）也是一种使用近似最近邻搜索的索引技术。它的特点是快速，同时仍然提供一个近似、非穷举的结果。LSH 使用一组哈希函数将相似向量映射到“桶”中，从而使相似向量具有相同的哈希值。这样，就可以通过比较哈希值来判断向量之间的相似度。

通常，我们设计的哈希算法都是力求减少哈希碰撞的次数，因为哈希函数的搜索时间复杂度是 O(1)，但是，如果存在哈希碰撞，即两个不同的关键字被映射到同一个桶中，那么就需要使用链表等数据结构来解决冲突。在这种情况下，搜索的时间复杂度通常是 O(n)，其中n是链表的长度。所以为了提高哈希函数的搜索的效率，通常会将哈希函数的碰撞概率尽可能的小。

但是在向量搜索中，我们的目的是为了找到相似的向量，所以可以专门设计一种哈希函数，使得哈希碰撞的概率尽可能高，并且位置越近或者越相似的向量越容易碰撞，这样相似的向量就会被映射到同一个桶中。

等搜索特定向量时，为了找到给定查询向量的最近邻居，使用相同的哈希函数将类似向量“分桶”到哈希表中。查询向量被散列到特定表中，然后与该表中的其他向量进行比较以找到最接近的匹配项。这种方法比搜索整个数据集要快得多，因为每个哈希表桶中的向量远少于整个空间中的向量数。

那么这个哈希函数应该如何设计呢？为了大家更好理解，我们先从二维坐标系解释，如下所图示，在二维坐标系中可以通过随机生成一条直线，将二维坐标系划分为两个区域，这样就可以通过判断向量是否在直线的同一边来判断它们是否相似。例如下图通过随机生成 4 条直线，这样就可以通过 4 个二进制数来表示一个向量的位置，例如 A 和 B 表示向量在同一个区域。

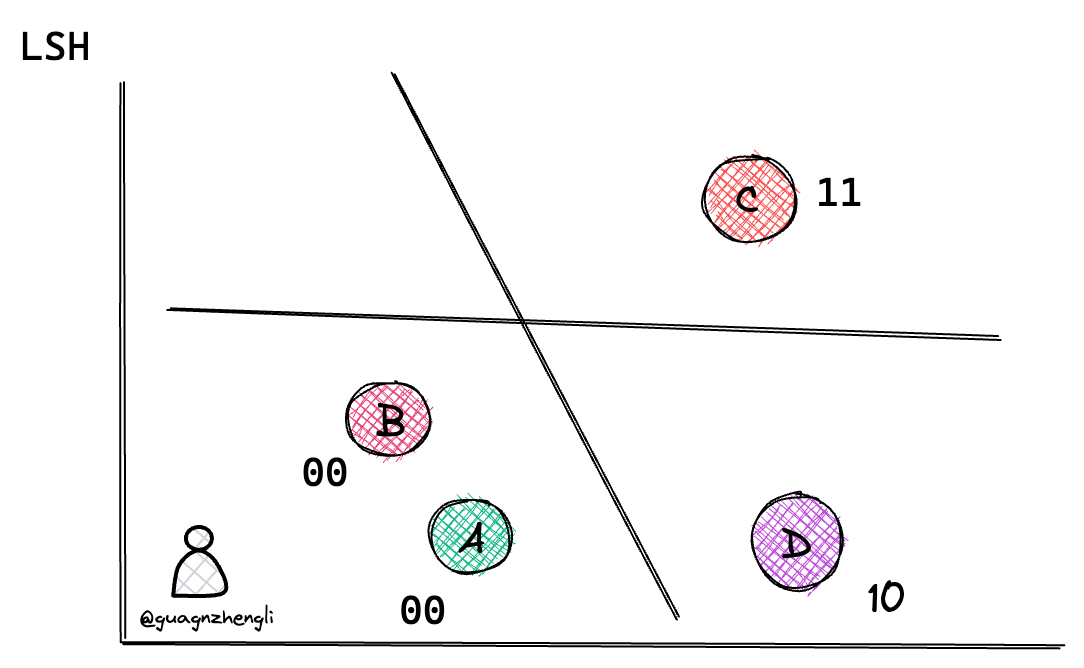
这个原理很简单，如果两个向量的距离很近，那么它们在直线的同一边的概率就会很高，例如直线穿过 AC 的概率就远大于直线穿过 AB 的概率。所以 AB 在同一侧的概率就远大于 AC 在同一侧的概率。

当搜索一个向量时，将这个向量再次进行哈希函数计算，得到相同桶中的向量，然后再通过暴力搜索的方式，找到最接近的向量。如下图如果再搜索一个向量经过了哈希函数，得到了 10 的值，就会直接找到和它同一个桶中相似的向量 D。从而大大减少了搜索的时间。

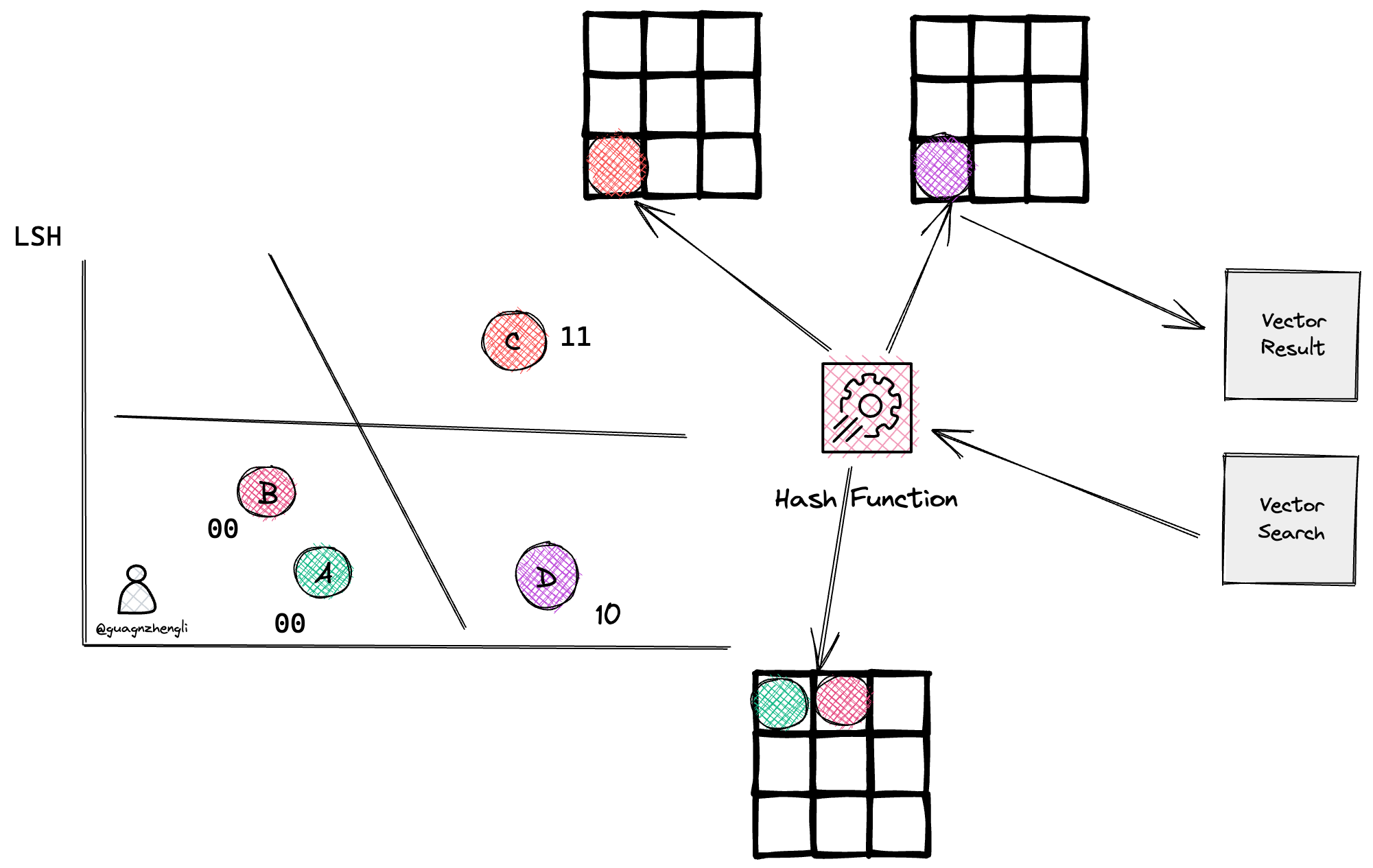
关于更多 LSH 算法的细节，可以参考这篇博客。

Random Projection for LSH 随机投影

如果在二维坐标系可以通过随机生成的直线区分相似性，那么同理，在三维坐标系中，就可以通过随机生成一个平面，将三维坐标系划分为两个区域。在多维坐标系中，同样可以通过随机生成一个超平面，将多维坐标系划分为两个区域，从而区分相似性。

但是在高维空间中，数据点之间的距离往往非常稀疏，数据点之间的距离会随着维度的增加呈指数级增长。导致计算出来的桶非常多，最极端的情况是每个桶中就一个向量，并且计算速度非常慢。所以实际上在实现 LSH 算法的时候，会考虑使用随机投影的方式，将高维空间的数据点投影到低维空间，从而减少计算的时间和提高查询的质量。

随机投影背后的基本思想是使用随机投影矩阵将高维向量投影到低维空间中。创建一个由随机数构成的矩阵，其大小将是所需的目标低维值。然后，计算输入向量和矩阵之间的点积，得到一个被投影的矩阵，它比原始向量具有更少的维度但仍保留了它们之间的相似性。

当我们查询时，使用相同的投影矩阵将查询向量投影到低维空间。然后，将投影的查询向量与数据库中的投影向量进行比较，以找到最近邻居。由于数据的维数降低了，搜索过程比在整个高维空间中搜索要快得多。

其基本步骤是：

从高维空间中随机选择一个超平面，将数据点投影到该超平面上。
重复步骤 1，选择多个超平面，将数据点投影到多个超平面上。
将多个超平面的投影结果组合成一个向量，作为低维空间中的表示。
使用哈希函数将低维空间中的向量映射到哈希桶中。

同样，随机投影也是一种近似方法，并且投影质量取决于投影矩阵。通常情况下，随机性越大的投影矩阵，其映射质量就越好。但是生成真正随机的投影矩阵可能会计算成本很高，特别是对于大型数据集来说。关于更多 RP for LSH 算法的细节，可以参考这篇博客。

相似性测量 (Similarity Measurement)

上面我们讨论了向量数据库的不同搜索算法，但是还没有讨论如何衡量相似性。在相似性搜索中，需要计算两个向量之间的距离，然后根据距离来判断它们的相似度。

而如何计算向量在高维空间的距离呢？有三种常见的向量相似度算法：欧几里德距离、余弦相似度和点积相似度。

欧几里得距离（Euclidean Distance）

欧几里得距离是指两个向量之间的距离，它的计算公式为：

其中，A 和 B 分别表示两个向量，�n 表示向量的维度。

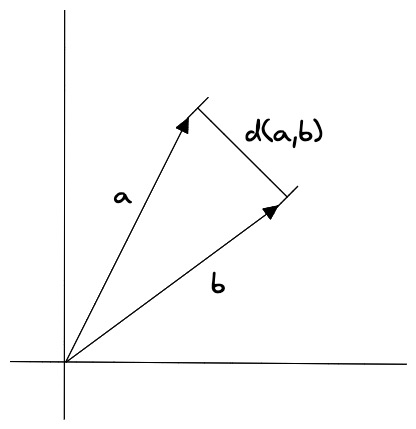
欧几里得距离算法的优点是可以反映向量的绝对距离，适用于需要考虑向量长度的相似性计算。例如推荐系统中，需要根据用户的历史行为来推荐相似的商品，这时就需要考虑用户的历史行为的数量，而不仅仅是用户的历史行为的相似度。

余弦相似度（Cosine Similarity）

余弦相似度是指两个向量之间的夹角余弦值，它的计算公式为：

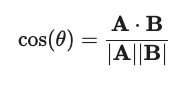
其中，A 和 B 分别表示两个向量，⋅⋅ 表示向量的点积，∣A∣ 和 ∣B∣ 分别表示两个向量的模长。

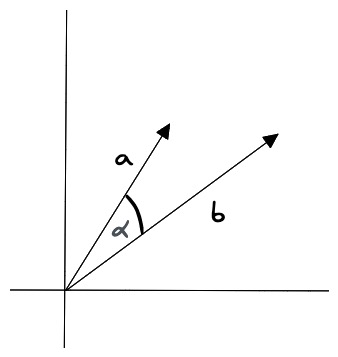
余弦相似度对向量的长度不敏感，只关注向量的方向，因此适用于高维向量的相似性计算。例如语义搜索和文档分类。

点积相似度 (Dot product Similarity)

向量的点积相似度是指两个向量之间的点积值，它的计算公式为：

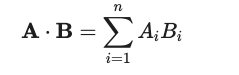
其中，A 和 B 分别表示两个向量，n 表示向量的维度。

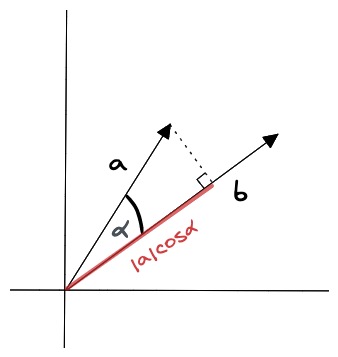
点积相似度算法的优点在于它简单易懂，计算速度快，并且兼顾了向量的长度和方向。它适用于许多实际场景，例如图像识别、语义搜索和文档分类等。但点积相似度算法对向量的长度敏感，因此在计算高维向量的相似性时可能会出现问题。

每一种相似性测量 (Similarity Measurement) 算法都有其优点和缺点，需要开发者根据自己的数据特征和业务场景来选择。

过滤 (Filtering)

在实际的业务场景中，往往不需要在整个向量数据库中进行相似性搜索，而是通过部分的业务字段进行过滤再进行查询。所以存储在数据库的向量往往还需要包含元数据，例如用户 ID、文档 ID 等信息。这样就可以在搜索的时候，根据元数据来过滤搜索结果，从而得到最终的结果。

为此，向量数据库通常维护两个索引：一个是向量索引，另一个是元数据索引。然后，在进行相似性搜索本身之前或之后执行元数据过滤，但无论哪种情况下，都存在导致查询过程变慢的困难。

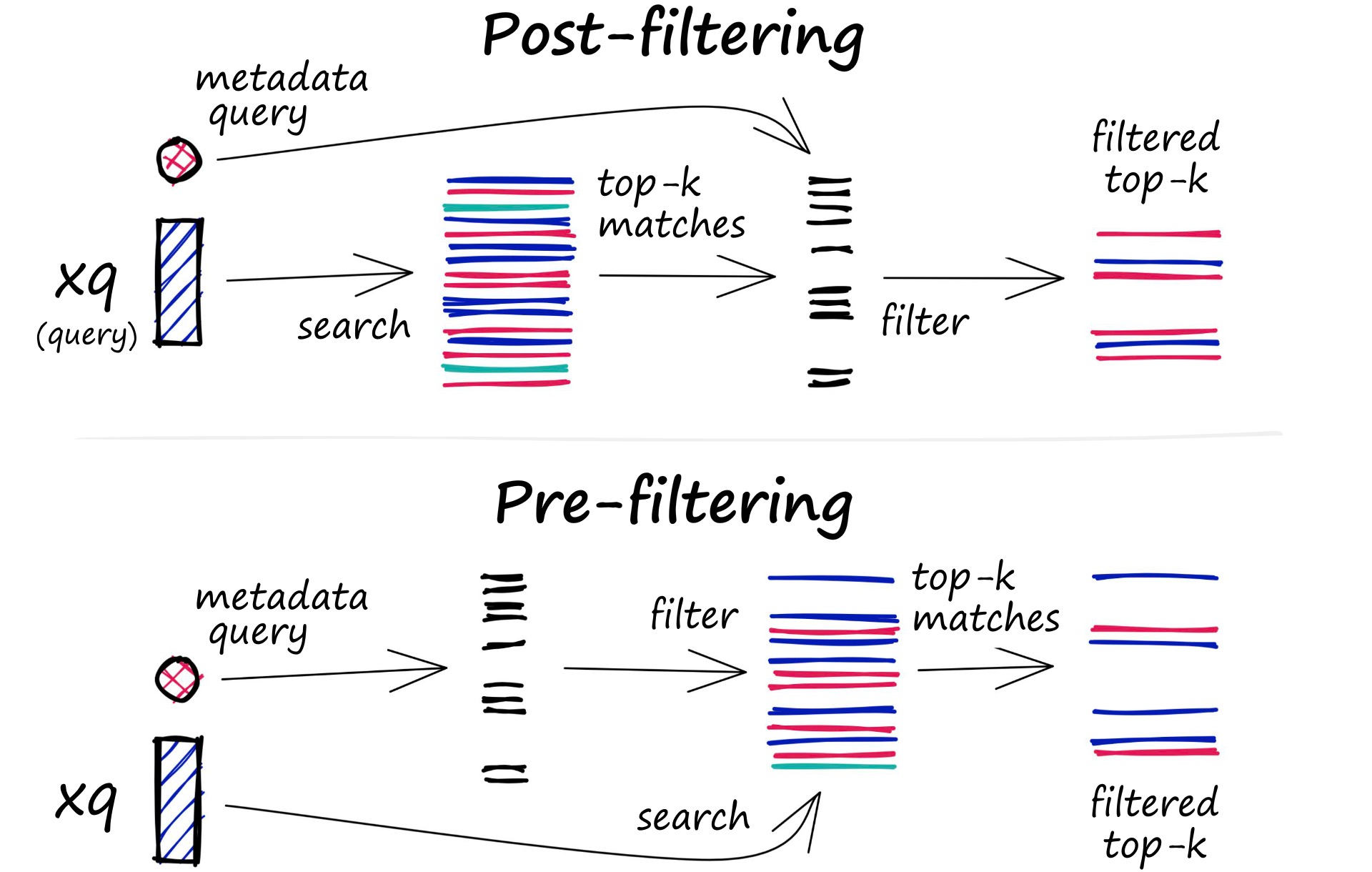
过滤过程可以在向量搜索本身之前或之后执行，但每种方法都有自己的挑战，可能会影响查询性能：

Pre-filtering：在向量搜索之前进行元数据过滤。虽然这可以帮助减少搜索空间，但也可能导致系统忽略与元数据筛选标准不匹配的相关结果。
Post-filtering：在向量搜索完成后进行元数据过滤。这可以确保考虑所有相关结果，在搜索完成后将不相关的结果进行筛选。

为了优化过滤流程，向量数据库使用各种技术，例如利用先进的索引方法来处理元数据或使用并行处理来加速过滤任务。平衡搜索性能和筛选精度之间的权衡对于提供高效且相关的向量数据库查询结果至关重要。

向量数据库选型

笔者在本文中，花费了大量的笔墨来介绍向量数据库的相似性搜索算法的原理和实现，相似性搜索算法固然是一个向量数据库的核心和关键点，但是在实际的业务场景中，往往还需要考虑其它的因素，例如向量数据库的可用性、扩展性、安全性等，还有代码是否开源、社区是否活跃等等。

分布式

一个成熟的向量数据库，往往需要支持分布式部署，这样才能满足大规模数据的存储和查询。数据拥有的越多，需要节点就越多，出现的错误和故障也就越多，所以分布式的向量数据库需要具备高可用性和容错性。

数据库的高可用性和容错性，往往需要实现分片和复制能力，在传统的数据库中，往往通过数据的主键或者根据业务需求进行分片，但是在分布式的向量数据库中，就需要考虑根据向量的相似性进行分区，以便查询的时候能够保证结果的质量和速度。

其它类似复制节点数据的一致性、数据的安全性等等，都是分布式向量数据库需要考虑的因素。

访问控制和备份

除此之外，访问控制设计的是否充足，例如当组织和业务快速发展时，是否能够快速的添加新的用户和权限控制，是否能够快速的添加新的节点，审计日志是否完善等等，都是需要考虑的因素。

另外，数据库的监控和备份也是一个重要的因素，当数据出现故障时，能够快速的定位问题和恢复数据，是一个成熟的向量数据库必须要考虑的因素。

API & SDK

对比上面的因素选择，API & SDK 可能是往往被忽略的因素，但是在实际的业务场景中，API & SDK 往往是开发者最关心的因素。因为 API & SDK 的设计直接影响了开发者的开发效率和使用体验。一个优秀良好的 API & SDK 设计，往往能够适应需求的不同变化，向量数据库是一个新的领域，在如今大部分人不太清楚这方面需求的当下，这一点容易被人忽视。

选型

截至目前，汇总到目前的向量数据库有以下几种选择：

向量数据库	URL	GitHub Star	Language	Cloud
chroma	https://github.com/chroma-core/chroma	7.4K	Python	❌
milvus	https://github.com/milvus-io/milvus	21.5K	Go/Python/C++	✅
pinecone	https://www.pinecone.io/	❌	❌	✅
qdrant	https://github.com/qdrant/qdrant	11.8K	Rust	✅
typesense	https://github.com/typesense/typesense	12.9K	C++	❌
weaviate	https://github.com/weaviate/weaviate	6.9K	Go	✅

传统数据的扩展

除了选择专业的向量数据库，使用传统数据库进行扩展也是一种方法。类似 Redis 除了传统的 Key Value 数据库用途外，Redis 还提供了 Redis Modules，这是一种通过新功能、命令和数据类型扩展 Redis 的方式。例如使用 RediSearch 模块来扩展向量搜索的功能。

同理的还有 PostgreSQL 的扩展，PostgreSQL 提供使用 extension 的方式来扩展数据库的功能，例如 pgvector 来开启向量搜索的功能。它不仅支持精确和相似性搜索，还支持余弦相似度等相似性测量算法。最重要的是，它是附加在 PostgreSQL 上的，因此可以利用 PostgreSQL 的所有功能，例如 ACID 事务、并发控制、备份和恢复等。还拥有所有的 PostgreSQL 客户端库，因此可以使用任何语言的 PostgreSQL 客户端来访问它。可以减少开发者的学习成本和服务的维护成本。

像笔者的开源项目 ChatFiles 和 VectorHub 目前就暂时使用 pgvector 来实现向量搜索以实现 GPT 文档问答，基于 Supabase 提供的 PostgreSQL + pgvector 服务完成。

总结

本文主要介绍了向量数据库的原理和实现，包括向量数据库的基本概念、相似性搜索算法、相似性测量算法、过滤算法和向量数据库的选型等等。向量数据库是崭新的领域，目前大部分向量数据库公司的估值乘着 AI 和 GPT 的东风从而飞速的增长，但是在实际的业务场景中，目前向量数据库的应用场景还比较少，抛开浮躁的外衣，向量数据库的应用场景还需要开发者们和业务专家们去挖掘。

References

转载自：https://guangzhengli.com/blog/zh/vector-database/#%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E8%B7%9D%E7%A6%BBeuclidean-distance

https://github.com/pgvector/pgvector